Cournot Rationalizability and Measurement Error

Abstract

This paper introduces measurement error to the Revealed Preference test of the Cournot Model. In contrast to the standard approach, the Revealed Preference analysis relies only on shape restrictions, i.e., the convexity of the firm’s cost function, but otherwise, no parametric assumptions are needed. In the application for the international market of crude oil, measurement errors might arise in the production quantities data due to the consolidation of information or coordination mistakes. Once measurement error is incorporated, the method requires a centering condition. Here, I assume that the quantity mismeasurement is uncorrelated with prices. In contrast to the deterministic version of the test, the Cournot model hypothesis can no longer be rejected.

Introduction

Testing firm conduct has been a long-standing question in the field of Industrial Organization. Do firms compete in prices or quantities? Do they exert market power? If firms have market power, what are the losses in consumer welfare? How big are the inefficiencies in the market? The answers to these questions are relevant not only to policymakers and regulating agencies but to the public in general.

A popular way to test a hypothesis about firm conduct is to use a discrete choice model to estimate demand in combination with an oligopoly model of supply. Typically, the practitioner must assume functional form restrictions and parametric distributions to estimate these models. However, an important question is how much of the results are driven by these functional forms and distributional assumptions.

An alternative approach is the Revealed Preference (RP) test. The RP analysis can be used to derive testable implications of a theoretical model and empirically assess its consistency with observational data. These tests commonly rely only on shape restrictions, but otherwise, no parametric assumptions are needed.

However, one of the main limitations of the way that this method is applied is that it cannot account for measurement error (ME). This is important because mismeasurements can potentially affect the test rejection rate. Intuitively, the RP test asks if there exists a convex cost function that rationalizes the data. If the model does not accommodate for randomness, the cost function has to pass through every data point. Therefore, as the observations increase, it is less likely that there exists a cost function that rationalizes the data.

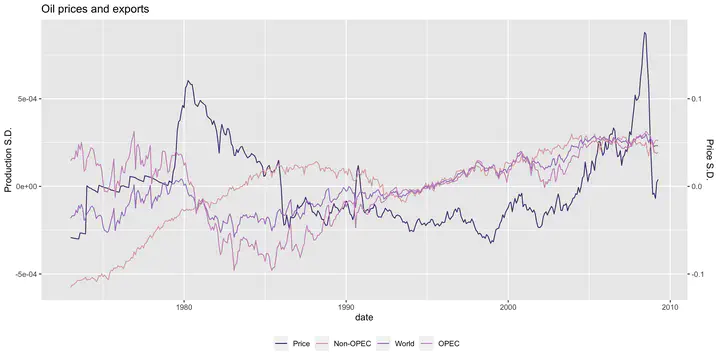
Consider the case of the Cournot competition model. In this model, firms compete in quantities and they produce a single homogeneous good with a downward sloping inverse demand function. It can be argued that the oil industry fits this setting. However, using data from oil-producing countries both within and outside the Organization of Petroleum Exporting Countries (OPEC) and employing the deterministic RP test, Carvajal et al. ( Citation: 2013 Carvajal, A., Deb, R., Fenske, J. & Quah, J. (2013). Revealed Preference Tests of the Cournot Model. Econometrica, 81(6). 2351–2379. https://doi.org/10.3982/ecta10175 ) reject the hypothesis that firms compete à la Cournot. Although the authors claim that the rejection provides evidence that firms’ interaction takes a more complicated form, it can also be the result of missing to incorporate measurement error.

This paper develops a method to introduce ME to the RP test of the Cournot Model. Using data on oil production volumes and prices for OPEC and major non-OPEC countries between 1973 and 2008, I ask whether the observed variables arise as a Cournot equilibrium if there is ME in the reported quantities. The method only requires a centering condition. Here, I assume that the semiannual average of the observed quantities is correct, and, importantly, the ME is uncorrelated with prices.

I find robust evidence that the Cournot hypothesis cannot be rejected even at the 10% significance level. The result stands at odds with the previous conclusion of the deterministic test. Thus, ignoring ME leads to an over-rejection of the RP test of oligopoly models, as is also the case on the consumer side ( Citation: Aguiar & Kashaev, 2020 Aguiar, V. & Kashaev, N. (2020). Stochastic revealed preferences with measurement error. Review of Economic Studies, 0. 1–52. https://doi.org/10.1093/restud/rdaa067 ) .

Moreover, this result is a first step towards assessing the question of how much is driven by the parametric restrictions of the traditional approach. I discuss the future work derived from this paper, including a non-parametric test for market power and non-parametric bounds for markups and marginal costs.

References